零知识证明与分布式计算的深度结合:将如何解锁下一个万亿赛道?
作者:火必研究院&谢锦斌(X Research DAO)
编辑: AndyHoo(X Research DAO)
1. 分布式计算发展历史和市场前景
1.1 发展历史
- 最开始的计算机每台只能执行一个计算任务,随着多核心多线程的CPU出现,单个计算机可以执行多个计算任务。
- 随着大型网站的业务增加,单服务器模式很难进行扩容,又增加硬件成本。面向服务的架构出现,由多台服务器组成。由服务注册者、服务提供者和服务消费者,三者组成。
- 但是随着业务增加和服务器增加,SOA模式下,点对点服务可维护性和可拓展性难度增加。类似微机原理中,总线模式出现,来协调各个服务单元。服务总线通过类似集线器的架构将所有系统连接在一起。这个组件被称为 ESB(企业服务总线)。作为一个中间角色,来翻译协调各个不同格式或者标准的服务协议。
- 随后基于应用程序编程接口(API)的 REST 模型通信,以其简洁、可组合性更高的特性,脱颖而出。各个服务以REST形式对外输出接口。当客户端通过 RESTful API 提出请求时,它会将资源状态表述传递给请求者或终端。该信息或表述通过 HTTP 以下列某种格式传输:JSON(Javascript 对象表示法)、HTML、XLT、Python、PHP 或纯文本。JSON 是最常用的编程语言,尽管它的名字英文原意为“JavaScript 对象表示法”,但它适用于各种语言,并且人和机器都能读。
- 虚拟机、容器技术,以及谷歌的三篇论文:
2003年,
2004年,
2006年,
- 分别是分布式文件系统、分布式计算、分布式数据库,拉开了分布式系统的帷幕。 Hadoop对谷歌论文的复现,更快更容易上手的Spark,满足实时计算的Flink。
- 但是以往都是分布式系统,并不是完全意义上的Peer to peer系统。在Web3领域,完全颠覆以往的软件架构。分布式系统的一致性,防欺诈攻击,防粉尘交易攻击等等一系列问题,都给去中心化计算框架带来挑战。
- 将以太坊为代表的智能合约公链,可以抽象理解为去中心化的计算框架,只不过EVM是有限指令集的虚拟机,无法做Web2需要的通用计算。而且链上资源也是极其昂贵。尽管如此,以太坊也是突破了点对点计算框架的瓶颈,点对点通信、计算结果全网一致性和数据一致性等等问题。
1.2 市场前景
读者在上面了解了分布式计算的历史,但还是会存在很多困惑,我来替读者列出大家可能存在的潜在疑问,如下:
从业务需求出发,为什么去中心化计算网络很重要?整体市场规模有多大?现在处于什么阶段,未来还有多少空间?哪些机会值得关注?怎么去赚钱?
1.2.1 为什么去中心化计算很重要?
在以太坊最初的愿景中,是要成为世界的计算机。在2017年,ICO大爆发之后,大家发现还是主要以资产发行为主。但是到了2020年,Defi summer出现,大量Dapp开始涌现。链上数据爆炸,面对越来越多复杂的业务场景,EVM越来越显得无力。需要链下拓展的形式,来实现EVM无法实现的功能。诸如像预言机等等角色,都是某种程度上的去中心化计算。
我们再以拓展思路去思考,现在Dapp高速增长,数据量也在爆炸式增长,这些数据的价值都需要更加复杂的算法来去计算,挖掘其商业价值。数据的价值由计算来体现和产生。这些都是大部分智能合约平台无法去实现的。
现在Dapp开发已经过去当初只需要完成0到1的过程,现在需要更加强大的底层设施,来支撑它完成更加复杂的业务场景。整个Web3已经从开发玩具应用阶段过去,未来需要面对更加复杂的逻辑和业务场景。
1.2.2 整体市场规模有多大?
如何估算市场规模呢?通过Web2领域的分布式计算业务规模来估算?乘上web3市场的渗透率?把目前市面上相应融资项目的估值相加吗?
我们不能将Web2的分布式计算市场规模照搬到Web3,理由是:1,Web2领域的分布式计算满足了大部分需求,Web3领域的去中心化计算是差异化满足市场需求。如果照搬,是有悖于市场客观背景环境。2,Web3领域的去中心化计算,未来成长出的市场业务范围是全球化的。所以我们需要更加严谨得去估算市场规模。
对于Web3领域潜在赛道整体规模预算通过以下几点出发来进行计算:
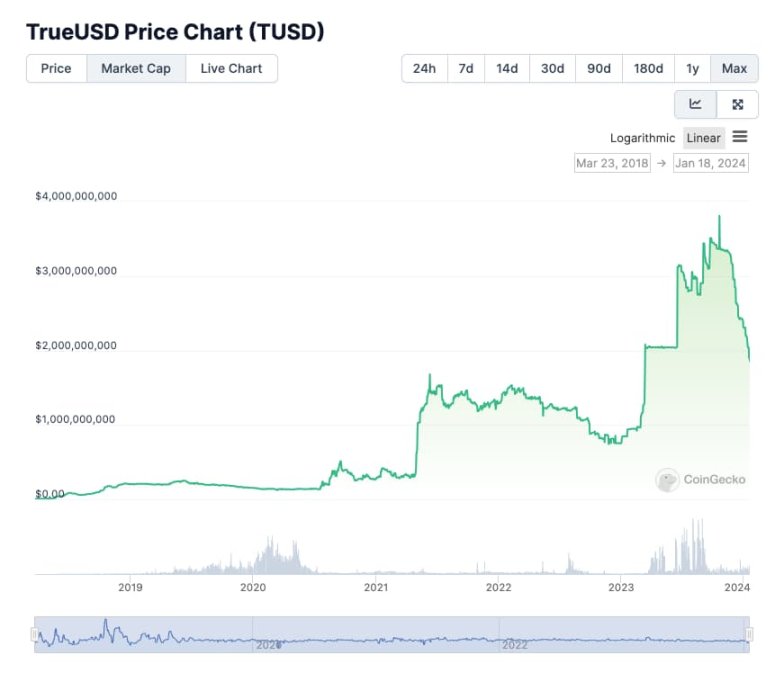
1.对行业内,其他可被纳入赛道范围内的项目估值,做为基准市值。 依据coinmarketcap网站上数据显示,在市面上已经流通的分布式计算板块的项目市值在67亿美元。
2.营收模型来自于,代币经济模型的设计,例如目前比较普遍流行的代币营收模型是,代币作为交易时候支付手续费的手段。所以可以通过手续费收入,间接反映生态的繁荣程度,交易活跃程度。最终作为估值评断的标准。当然,token还有其他成熟的模型,例如用于抵押挖矿,或者交易的交易对,或者是算法稳定币的锚定资产。所以Web3项目的估值模型,区别于传统股票市场,更像是国家货币。代币可以被采用的场景会有多样性。所以对于具体项目具体分析。我们可以尝试探索Web3去中心化计算场景中,代币模型应该如何进行设计。首先我们假定自己去设计一个去中心化计算框架,我们会遇到什么样的挑战?a).因为完全去中心化的网络,在这样不可信的环境中完成计算任务的执行,需要激励资源提供者保障在线率,还要保障服务质量。在博弈机制上,需要保证激励机制合理,还要如何防止攻击者发起欺诈攻击、女巫攻击等等攻击手段。所以需要代币作为质押手段参与POS共识网络,先保障所有节点的共识一致性。对于资源贡献者,需要其贡献的工作量来实施一定的激励机制,代币激励对业务增加和网络效率提升,必须要有正向循环增长的。b).相较于其他layer1,网络本身也会产生大量交易,面对大量粉尘交易,每笔交易支付手续费,是经过市场验证的代币模型。c).如果代币只是实际用途化,市值是很难再进一步扩大。如果作为资产组合的锚定资产,进行几层资产嵌套组合,极大扩张金融化的效果。整体估值=质押率*Gas消耗率*(流通量的倒数)*单个价格
1.2.3 现在处于什么阶段,未来还有多少空间?
2017年到现在,很多团队都在尝试去中心化计算方向上发展,但是都尝试失败,后面会具体解释失败的原因。探索路径由最初类似外星人探索计划的项目,后来发展到模仿传统云计算的模式,再到Web3原生模式的探索。
当前整个赛道的现状,处于在学术层面已经验证0到1的突破,一些大型项目在工程实践上,有了较大的进展。例如当前的zkRollup和zkEVM实现上,都是刚刚发布产品的阶段。
未来还有很大空间,理由如下:1,还需提升验证计算的高效性。2,还需要补充丰富更多指令集。3,真正不同业务场景的优化。4,以往用智能合约无法实现的业务场景,可以通过去中心化计算实现。
我们通过一个具体案例来解释,完全去中心化的游戏。目前大部分Gamefi需要一个中心化服务做为后端,其后端作用在于管理玩家的状态数据和一些业务逻辑,其应用前端在于用户交互逻辑和事件触发后传递到后端。当前市面上还没有完整的解决方案,可以支撑Gamefi的业务场景。但是可被验证的去中心化计算协议出现,后端替换为zkvm。可以真正实现去中心化的游戏。前端将用户事件逻辑,发送到zkvm执行相关业务逻辑,被验证后,在去中心化数据库记录状态。
当然这只是提出的一个应用场景,而Web2有很多业务场景需要计算的能力。
1.2.4 哪些机会值得关注?怎么去赚钱?
|
应用场景虚拟机类型 |
通用型高性能虚拟机 |
AI虚拟机 |
|
DeFi |
金融数据处理/高并发金融交易并行执行确认/高性能撮合。。。 |
人脸识别/信用评估/为更多借贷业务服务。。。 |
|
NFT |
省Gas聚合交易/批量注册任务 |
AIGC/价值估算。。 |
|
社交应用 |
迁移Web2的社交应用/高并发高并行的业务场景/基本的社交业务逻辑,之前智能合约无法实现的 |
推荐算法。。。 |
|
gamefi |
去中心化游戏/多人在线网络通信处理… |
防作弊 |
|
创作者经济 |
对于不同文件类型的内容创作平台,需要支撑其业务逻辑执行的虚拟机 |
AIGC |
2. 去中心化的分布式计算尝试
2.1云服务模式
目前以太坊有如下问题 :
1.整体吞吐量低。消耗了大量的算力,但是吞吐量只相当于一台智能手机。
2.验证积极性低。这个问题被称为 Verifier's Dilemma。获得打包权的节点得到奖励,其他节点都需要验证,但是得不到奖励,验证积极性低。久而久之,可能导致计算得不到验证,给链上数据安全性带来风险。
3.计算量受限 (gasLimit),计算成本较高。
有团队尝试采用,被Web2广泛采用的云计算模式。用户支付一定费用,按照计算资源使用时间来计算费用。采取这样模式,其根本原因是因为其无法验证计算任务是否被正确执行,只能通过可检测的时间参数或者其他可控的参数。
最终这个模式没有广泛应用,没有考虑人性的因素。大量资源被用于挖矿,以谋取最大利益。导致真正可被利用的资源较少。这是博弈系统内,各个角色谋求利益最大化的结果。
最终呈现的结果,和最开始的初衷完全背离。
2.2挑战者模式
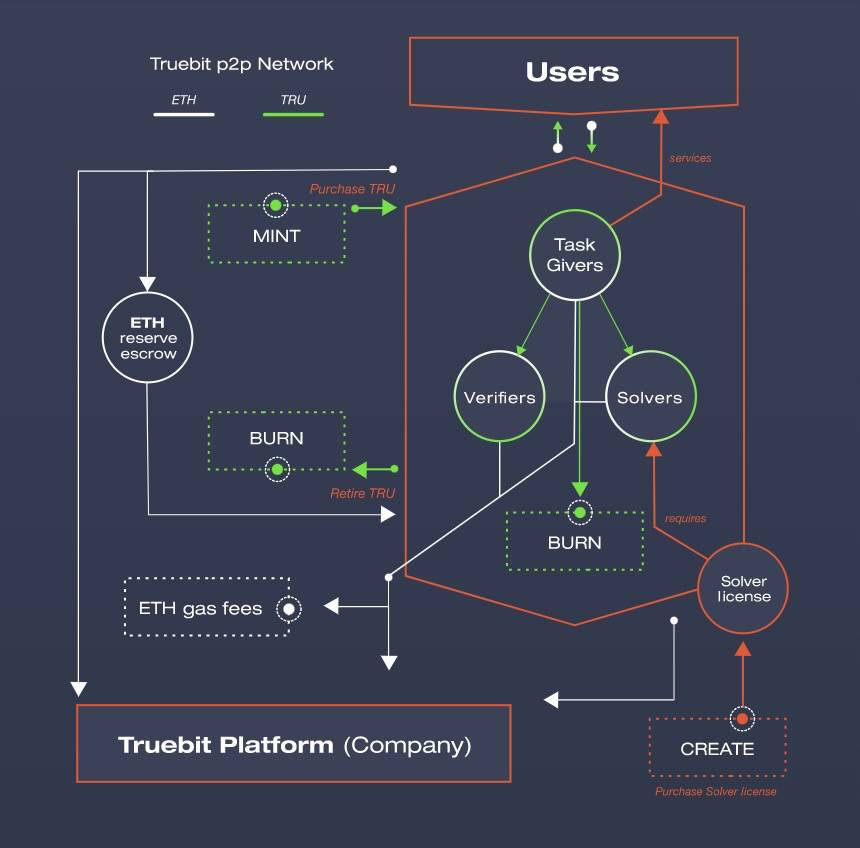
而TrueBit则利用博弈体系,达到全局最优解,来保障下发的计算任务是被正确执行。
我们快速这种计算框架的核心要点:
1.角色:问题解决者、挑战者和法官
2.问题解决者需要质押资金,才可以参与领取计算任务
3.挑战者作为赏金猎人,需要重复验证问题解决者的计算结果,和自己本地的是否一致
4.挑战者会去抽取与两者计算状态一致的最近时间的计算任务,如果出现分歧点,提交分歧点的默克树hash值
5.最后法官评判是否挑战成功
但是这个模式存在以下几点缺陷:
1.挑战者可以晚时间提交,只需要完成提交任务就行。这样导致结果是,缺少及时性。
2.3利用零知识证明验证计算
所以如何实现,既保证计算过程可被验证,又能保障验证的及时性。
例如zkEVM的实现,每个区块时间,需要提交可被验证的zkProof。这个zkProof包含逻辑计算业务代码生成的字节码,再由字节码执行生成电路代码。这样实现了计算业务逻辑是被正确执行,而且通过较短和固定时间来保障验证的及时性。
虽然zkEVM只是针对智能合约执行的场景,本质还是在计算业务框架下面。如果我们将EVM逻辑顺延到其他通用类型的虚拟机,例如WASM虚拟机,或者更加通用的LLVM高性能虚拟机。当然在具体落实到工程实践上会有诸多挑战,却给我们更多的探索空间。
在假定条件下,有足够高性能的零知识证明加速硬件和足够被优化的零知识证明算法,通用计算场景可以得到充分发展。大量Web2场景下的计算业务,都可以被零知识证明通用虚拟机进行复现。就如前文所提到可赚钱的业务方向。
3. 零知识证明和分布式计算的结合
3.1 学术层面
我们回看一下零知识证明算法历史发展演进的路线
1.GMR85是最早起源的算法,来源于 Goldwasser、Micali 和 Rackoff 合作发表的论文:The Knowledge Complexity of Interactive Proof Systems(即 GMR85),该论文提出于 1985 年,发表于 1989 年。这篇论文主要阐释的是在一个交互系统中,经过 K 轮交互,需要多少知识被交换,从而证明一个证言(statement)是正确的。
2.姚氏混淆电路(Yao's Garbled Circuit,GC)[89]。一种著名的基于不经意传输的两方安全计算协议,它能够对任何函数进行求值。混淆电路的中心思想是将计算电路(我们能用与电路、或电路、非电路来执行任何算术操作)分解为产生阶段和求值阶段。每一方都负责一个阶段,而在每一阶段中电路都被加密处理,所以任何一方都不能从其他方获取信息,但他们仍然可以根据电路获取结果。混淆电路由一个不经意传输协议和一个分组密码组成。电路的复杂度至少是随着输入内容的增大而线性增长的。在混淆电路发表后,Goldreich-Micali-Wigderson(GMW)[91]将混淆电路扩展使用于多方,用以抵抗恶意的敌手。
3.sigma协议又称为诚实验证者的(特殊)零知识证明。即假设验证者是诚实的。这个例子类似Schnorr身份认证协议,只是后者通常采用非交互的方式。
4.2013 年的 Pinocchio (PGHR13):Pinocchio: Nearly Practical Verifiable Computation,将证明和验证时间压缩到适用范围,也是 Zcash 使用的基础协议。
5.2016 年 的 Groth16:On the Size of Pairing-based Non-interactive Arguments,精简了证明的大小,并提升了验证效率,是目前应用最多的 ZK 基础算法。
6.2017 年的 Bulletproofs (BBBPWM17) Bulletproofs: Short Proofs for Confidential Transactions and More,提出了 Bulletproof 算法,非常短的非交互式零知识证明,不需要可信的设置,6 个月以后应用于 Monero,是非常快的理论到应用的结合。
7.2018 年 的 zk-STARKs (BBHR18) Scalable, transparent, and post-quantum secure computational integrity,提出了不需要可信设置的 ZK-STARK 算法协议,这也是目前 ZK 发展另一个让人瞩目的方向,也以此为基础诞生了 StarkWare 这个最重量级的 ZK 项目。
8.Bulletproofs的特点为:
1)无需trusted setup的short NIZK
2)基于Pedersen commitment构建
3)支持proof aggregation
4)Prover time为:O ( N ⋅log ( N ) ) O(Ncdot log(N))O(N⋅log(N)),约30秒
5)Verifier time为:O ( N ) O(N)O(N),约1秒
6)proof size为:O ( log ( N ) ) O(log(N))O(log(N)),约1.3KB
7)基于的安全假设为:discrete log
Bulletproofs适用的场景为:
1)range proofs(仅需约600字节)
2)inner product proofs
3)MPC协议中的intermediary checks
4)aggregated and distributed (with many private inputs) proofs
9.Halo2主要特点为:
1)无需trusted setup,将accumulation scheme 与 PLONKish arithmetization高效结合。
2)基于IPA commitment scheme。
3)繁荣的开发者生态。
4)Prover time为:O ( N ∗log N ) O(N*log N)O(N∗logN)。
5)Verifier time为:O ( 1 ) > O(1)>O(1)>Groth16。
6)Proof size为:O ( log N ) O(log N)O(logN)。
7)基于的安全假设为:discrete log。
Halo2适于的场景有:
1)任意可验证计算
2)递归proof composition
3)基于lookup-based Sinsemilla function的circuit-optimized hashing
Halo2不适于的场景为:
1)除非替换使用KZG版本的Halo2,否则在以太坊上验证开销大。
10.Plonky2主要特点为:
1)无需trusted setup,将FRI与PLONK结合。
2)针对具有SIMD的处理器进行了优化,并采用了64 byte Goldilocks fields。
3)Prover time为:O ( log N ) O(log N)O(logN)。
4)Verifier time为:O ( log N ) O(log N)O(logN)。
5)Proof size为:O ( N ∗log N ) O(N*log N)O(N∗logN)。
6)基于的安全假设为:collision-resistant hash function。
Plonky2适于的场景有:
1)任意可验证计算。
2)递归proof composition。
3)使用自定义gate进行电路优化。
Plonky2不适于的场景为:
1)受限于其non-native arithmetic,不适于包含椭圆曲线运算的statements。
目前Halo2成为zkvm采用的主流算法,支持递归证明,支持验证任意类型的计算。为零知识证明类型虚拟机做通用计算场景,奠定了基础。
3.2工程实践层面
既然零知识证明在学术层面突飞猛进,具体落地到实际开发时候,目前进展是怎样的呢?
我们从多个层面去观察:
- 编程语言:目前有专门的编程语言,帮助开发者不需要深入了解电路代码如何设计,这样就可以降低开发门槛。当然也有支持将Solidity转译成电路代码。开发者友好程度越来越高。
- 虚拟机:目前有多种实现的zkvm,第一种是自行设计的编程语言,通过自己的编译器编译成电路代码,最后生成zkproof。第二种是支持solidity编程语言,通过LLVM编译成目标字节码,最后转译成电路代码和zkproof。第三种是真正意义的EVM等效兼容,最终将字节码的执行操作,转译成电路代码和zkproof。目前是zkvm的终局之战吗?并没有,不管是拓展到智能合约编程之外的通用计算场景,还是不同方案的zkvm针对自身底层指令集的补齐和优化,都还是1到N的阶段。任重而道远,大量工程上的工作需要去优化和实现。各家在学术层到工程实现上实现了落地,谁能最终成为王者,杀出一条血路。不仅需要在性能提升有大幅进展,还要能吸引大量开发者进入生态。时间点是十分重要的前提要素,先行推向市场,吸引资金沉淀,生态内自发涌现的应用,都是成功的要素。
- 周边配套工具设施:编辑器插件支持、单元测试插件、Debug调试工具等等,帮助开发者更加高效的开发零知识证明应用。
- 零知识证明加速的基础设施:因为整个零知识证明算法中,FFT和MSM占用了大量运算时间,可以GPU/FPGA等并行计算设备来并行执行,达到压缩时间开销的效果。
- 不同编程语言实现:例如采用更加高效或者性能表现更好的编程语言:Rust。
- 明星项目涌现:zkSync、Starkware等等优质项目,相继宣布其正式产品发布的时间。说明了,零知识证明和去中心化计算结合不再是停留在理论层面,在工程实践上逐渐成熟。
4. 遇到的瓶颈以及如何解决
4.1 zkProof生成效率低
前面我们讲到,关于这块市场容量、目前行业发展情况、在技术上的实际进展,但是没有存在一点挑战吗?
我们对整个zkProof生成的流程进行拆解:
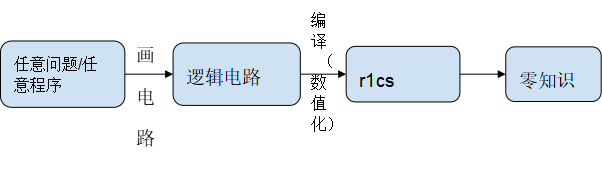
在逻辑电路编译数值化r1cs的阶段,里面80%的运算量在NTT和MSM等计算业务上。另外对逻辑电路不同层级进行hash算法,随着层级越多,Hash算法时间开销线性增加。当然现在行业内提出时间开销减少200倍的GKR算法。
但是NTT和MSM计算时间开销,还是居高不下。如果希望给用户减少等待时间,提升使用体验效果,必须要在数学实现上、软件架构优化、GPU/FPGA/ASIC等等层面进行加速。
下图为各个zkSnark家族算法的证明生成时间和验证时间的测试:
|
Benchmark Results |
|||||||
|
Sudoku: compile |
|||||||
|
Miden |
Plonk: 3 by 3 |
Risc |
Halo: 3 by 3 |
||||
|
1.52 ms (✅1.00x) |
99.92 ms (❌65.80x slower) |
1.86 ms (❌1.22x slower) |
329.15 ms (❌216.76x slower) |
||||
|
Sudoku: prove |
|||||||
|
Miden |
Plonk: 3 by 3 |
Risc |
Halo: 3 by 3 |
||||
|
477.41 ms (✅1.00x) |
100.52 ms (���4.75x faster) |
1.67 s (❌3.49x slower) |
116.74 ms (���4.09x faster) |
||||
|
Sudoku: verify |
|||||||
|
Miden |
Plonk: 3 by 3 |
Risc |
Halo: 3 by 3 |
||||
|
2.41 ms (✅1.00x) |
7.28 ms (❌3.02x slower) |
2.79 ms (❌1.15x slower) |
4.39 ms (❌1.82x slower) |
||||
|
Sudoku: |
|||||||
|
Miden |
Plonk: 3 by 3 |
Risc |
Halo: 3 by 3 |
||||
|
475.69 ms (✅1.00x) |
205.22 ms (���2.32x faster) |
1.67 s (❌3.52x slower) |
450.98 ms (✅1.05x faster) |
||||
|
fibonacci: compile |
|||||||
|
Miden: iter-93 |
Miden: fixed-92 |
Miden: fixed-50 |
Risc0: iter-93 |
Risc0: iter-50 |
Risc0: fixed-50 |
Risc0: fixed-92 |
|
|
64.89 us (✅1.00x) |
55.92 us (✅1.16x faster) |
45.01 us (✅1.44x faster) |
387.69 us (❌5.97x slower) |
388.34 us (❌5.98x slower) |
391.42 us (❌6.03x slower) |
390.26 us (❌6.01x slower) |
|
|
fibonacci: prove |
|||||||
|
Miden: iter-93 |
Miden: fixed-92 |
Miden: fixed-50 |
Risc0: iter-93 |
Risc0: iter-50 |
Risc0: fixed-50 |
Risc0: fixed-92 |
|
|
472.51 ms (✅1.00x) |
231.76 ms (���2.04x faster) |
233.25 ms (���2.03x faster) |
417.66 ms (✅1.13x faster) |
413.46 ms (✅1.14x faster) |
410.38 ms (✅1.15x faster) |
412.02 ms (✅1.15x faster) |
|
|
fibonacci: verify |
|||||||
|
Miden: iter-93 |
Miden: fixed-92 |
Miden: fixed-50 |
Risc0: iter-93 |
Risc0: iter-50 |
Risc0: fixed-50 |
Risc0: fixed-92 |
|
|
2.41 ms (✅1.00x) |
2.36 ms (✅1.02x faster) |
2.36 ms (✅1.02x faster) |
2.55 ms (✅1.06x slower) |
2.55 ms (✅1.06x slower) |
2.55 ms (✅1.06x slower) |
2.55 ms (✅1.06x slower) |
|
|
fibonacci: |
|||||||
|
Miden: iter-93 |
Miden: fixed-92 |
Miden: fixed-50 |
Risc0: iter-93 |
Risc0: iter-50 |
Risc0: fixed-50 |
Risc0: fixed-92 |
|
|
475.43 ms (✅1.00x) |
234.39 ms (���2.03x faster) |
235.84 ms (���2.02x faster) |
421.28 ms (✅1.13x faster) |
417.20 ms (✅1.14x faster) |
413.70 ms (✅1.15x faster) |
415.58 ms (✅1.14x faster) |
|
|
fibonacci large: compile |
|||||||
|
Miden: iter-1000 |
Risc0: iter-1000 |
||||||
|
64.91 us (✅1.00x) |
387.43 us (❌5.97x slower) |
||||||
|
fibonacci large: prove |
|||||||
|
Miden: iter-1000 |
Risc0: iter-1000 |
||||||
|
4.07 s (✅1.00x) |
3.39 s (✅1.20x faster) |
||||||
|
fibonacci large: verify |
|||||||
|
Miden: iter-1000 |
Risc0: iter-1000 |
||||||
|
2.66 ms (✅1.00x) |
2.96 ms (✅1.11x slower) |
||||||
|
fibonacci large: |
|||||||
|
Miden: iter-1000 |
Risc0: iter-1000 |
||||||
|
4.07 s (✅1.00x) |
3.40 s (✅1.20x faster) |
||||||
|
Blake: compile |
|||||||
|
Risc0: Library-The quick brown fox jumps over the lazy dog |
|||||||
|
466.84 us (✅1.00x) |
|||||||
|
Blake: prove |
|||||||
|
Risc0: Library-The quick brown fox jumps over the lazy dog |
|||||||
|
3.40 s (✅1.00x) |
|||||||
|
Blake: verify |
|||||||
|
Risc0: Library-The quick brown fox jumps over the lazy dog |
|||||||
|
4.24 ms (✅1.00x) |
|||||||
|
Blake: |
|||||||
|
Risc0: Library-The quick brown fox jumps over the lazy dog |
|||||||
|
3.40 s (✅1.00x) |
|||||||
|
Blake3: compile |
|||||||
|
Miden: Library-quick brown fox |
|||||||
|
7.38 ms (✅1.00x) |
|||||||
|
Blake3: prove |
|||||||
|
Miden: Library-quick brown fox |
|||||||
|
1.99 s (✅1.00x) |
|||||||
|
Blake3: verify |
|||||||
|
Miden: Library-quick brown fox |
|||||||
|
3.12 ms (✅1.00x) |
|||||||
|
Blake3: |
|||||||
|
Miden: Library-quick brown fox |
|||||||
|
2.01 s (✅1.00x) |
既然我们可以看到缺陷和挑战,同时也意味着其中深藏着机会:
1.设计针对特定zkSnark算法加速或者通用zkSnark算法加速的芯片。相比其他类型的加密算法,zkSnark产生较多临时文件,对于设备的内存和显存存在要求。芯片创业项目,同时也面临大量资金投入,还不一定能保障最后可以流片成功。但是一旦成功,其技术壁垒和IP保护都将是护城河。芯片项目创业,必须要足够议价能力的渠道,拿到最低成本。以及在整体品控上做到保障。
2.显卡加速的Saas服务,利用显卡做加速,是支出代价小于ASIC设计,而且开发周期也较短。但是软件创新上,在长周期上最终会被硬件加速所淘汰。
4.2 硬件资源占用大
目前和一些zkRollup项目接触,最终发现还是大内存和大显存显卡比较适合他们用于软件加速。例如在Filecoin挖矿中,大量闲置的数据封装机成为了现在热门zkRollup项目的目标设备。在Filecoin挖矿中,在C2阶段,需要将生成的电路代码文件,生成并缓存在内存中。如果业务代码逻辑十分复杂,其对应生成的电路代码规模也会非常大,最终呈现形式就是体积大的临时文件,特别涉及对电路代码进行Hash运算,需要AMD CPU指令来加速。因为直接CPU和内存之间高速交换,效率非常高。这里面还需要涉及到NVME的固态硬盘,都会是对zkSnark运算起到加速作用。以上我们对可能存在加速实现的可能性进行探讨,发现对资源要求还是非常高的。
在未来,如果想大规模普及zkSnark应用,通过不同层面优化,势在必行。
4.3 Gas消耗成本
我们观察到所有zkRollup Layer2需要将zkProof传递到layer1进行验证和存储,因为ETH链上资源十分昂贵,如果大规模普及后,需要为ETH支付大量Gas。最终由用户承担这个成本,和技术发展的初衷。
所以很多zkp项目提出,数据有效层、利用递归证明压缩提交的zkProof,这些都是为了降低Gas cost。
4.4 虚拟机的指令缺失
当前大部分zkvm面向智能合约编程的平台,如果要更加通用的计算场景,对zkvm底层指令集有大量的补齐工作。例如zkvm虚拟机底层支持libc指令,支持矩阵运算的指令,等等其他更加复杂的计算指令。
5. 结语
因为智能合约平台更多面向资产进行编程,如果我们希望更多真实业务场景可以接入到Web3,零知识证明和去中心化计算的结合带来了契机。我们相信零知识证明将会成为主流赛道,不再是细分领域的技术。